Една од предностите е можноста на експериментирање и прегледноста на експериментите коишто се направени. Друга предност се формулите коишто се дадени во симулацијата и со кои можеме полесно да ја извршиме саканата пресметка. Трета предност е графикот кој е тука.
Од оваа страница, одбрав две симулации кои според мене се поинтересни, подетални и поголеми од останатите.
1.
Една од симулациите која ја одбрав е Double Spring или симулација на двојна пружина.Во оваа симулација се дадени две пружини коишто се споени со ѕид, кој ја претставувa y оската. Со промена на вредностите можеме да експериментираме со:
-нивната маса ( mass-1 и mass-2 )
-нивната амортизација ( damping )
-должината на пружините ( spring length )
-еластичност на пружините ( spring stiffness )
-менување на временскиот чекор ( time step )
-временската стапка ( time rate )
-позадината ( background )
-методот на решавачот на диференцијални равенки, заменувајќи ги рунгe-кутовиот ( Runge-Kutta ) и еулеровиот метод ( Eulers method). Останатите методи се само опции и изведби од овие два оригинални методи
Освен тоа можеме:
-да додадеме уште една пружина ( со кликање на квадратот до "third spring" )
-да направиме да се гледа енергијата ( со кликање на квадратот до "show energy" )
-да измериме за колку време се одвива одредено движење ( со кликање на квадратот до
"show clock" )
-да го промениме начинот на којшто ја гледаме симулацијата ( со кликање на квадратот до
"pan-zoom" )
Доколку поради одредени причини сакаме да ја вратиме симулацијата во рамнотежна состојба, потребно е да кликнеме на

Преку равенките за движење во физиката, вклучувајќи ја и равенката на Исак Њутн, можеме лесно да ја пресметаме силата, масата и растојанието.
Освен тоа, можеме да пресметаме и брзина.
-Можеме да видиме и обичен график, временски график и мулти график, за подоброо мерење.
2.Другата симулација е "Single Spring" или симулација на единечна пружина
-нејзината маса ( mass)
-со нејзината амортизација ( damping )
-со нејзината еластичност ( spring stiffness )
-со нејзината должина ( spring length )
-со нејзината почетна точка ( fixed point )
-временската стапка ( time rate )
-позадината ( background )
-позадината ( background )
-методот на решавачот на диференцијални равенки, заменувајќи ги рунгe-кутовиот ( Runge-Kutta ) и еулеровиот метод ( Eulers method). Останатите методи се само опции и изведби од овие два оригинални методи
Освен тоа можеме:
-да направиме да се гледа енергијата ( со кликање на квадратот до "show energy" )
-да измериме за колку време се одвива одредено движење ( со кликање на квадратот до
"show clock" )
-да го промениме начинот на којшто ја гледаме симулацијата ( со кликање на квадратот до
"pan-zoom" )
Можеме да ги одговориме следните загатки:
-Која е врската помеѓу забрзување и помесувањето?
-Како масата или вкочанетоста на пружината влијае врз односот на забрзувањето и поместувањето?
-Како масата илии вкочанетоста на пружината влијае врз периодот или фреквенцијата од осцилацијата?
Одговори:
1. Тоа е линеарна врска дадена со равенката:
каде x= позицијата, x"= забрзувањето, m= масата и k= вкочанетоста на пружината
2. Од горенаведената задача знаеме дека е линерна врска, што значи дека масата и вкочанетоста на пружината влијае врз наклонот на оваа линија.
*Со зголемување на масата оваа линија е се помалку стрмна
*Со зголемување на вкочанетоста линија е се пострмна
3. Со формулата за преместување на поместувањето
и за фреквенцијата
може лесно да се дознае дека:
-со зголемување на масата за 4 пати го зголемува периодот два пати и ја преполовува фреквенцијата;
-со зголемување на вкочанетоста на пружината за 4 пати, се преполовува периодот и двојно се зголемува фреквенцијата
За поголема прегледност можат да се искористат и графиците, меѓу кои се:
-обичниот графикон
-временскиот графикон
-мулти графиконот




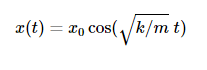




No comments:
Post a Comment
Note: only a member of this blog may post a comment.